In the first part of this piece I pointed out why it can be difficult to validate TAR using control set metrics. When the overall proportion of responsive documents is very low, it becomes increasingly burdensome to randomly sample enough documents for useful estimates of recall and precision. For this reason and others, elusion testing is joining or even displacing control set metrics as the industry’s preferred approach to validation.
Elusion testing is often preferable because it is easier and more intuitive to infer meaningful estimates from the resulting proportions, allows one to include all or nearly all reviewed material as training data, and may reduce the burden of reviewing a large volume of non-responsive documents for validation purposes.
In the context of eDiscovery, an elusion test sample is a random sample of all documents not slated for production or human review. The proportion of responsive documents in the sample serves to approximate the number of responsive documents in that discard pile. This is usually undertaken at the end of the review process as a means of confirming that a party has made a reasonable and proportional effort to satisfy their document production obligations.
Because recall and precision are calculated using only a subset of documents in a random sample, it can be difficult to determine how many total documents to include in a control set sample. However, since the proportion we’re estimating with elusion testing is taken from the full sample set used for validation, it is far easier to calculate an appropriate sample size.
That said, it’s just as dangerous to fixate on a certain sample size or confidence interval for elusion testing as it is to do so for a control set. Consider the following examples.
Imagine we’re faced with a review database consisting of:
| 150,000 Total Documents | ||
| 30,000 responsive documents prioritized by TAR software and coded with perfect accuracy by attorneys | 20,000 not responsive documents prioritized by TAR software and coded with perfect accuracy by attorneys | 100,000 documents categorized as unlikely to be responsive and not reviewed by attorneys |
Since our software indicates that the remaining 100,000 are not responsive, we decide to validate using elusion testing. We use the sampling feature of our software to specify a 95% confidence level (CL) and 5% confidence interval (CI) or margin of error (MoE) to randomly select 383 documents for our elusion test.
The review team codes with perfect accuracy and identifies 5 documents of the 383 as responsive. A conservative interval estimate using a 95% confidence level suggests that .4% to 3% of the not reviewed documents are responsive. This means we can expect to find an additional 400 to 3000 responsive documents in the not reviewed data.
Remembering that recall is the proportion of all responsive documents correctly identified as responsive, we can now estimate a range for this proportion using simple arithmetic.
This time we’re looking at:
| 150,000 Total Documents | ||
| 4,000 responsive documents prioritized by TAR software and coded with perfect accuracy by attorneys | 46,000 not responsive documents prioritized by TAR software and coded with perfect accuracy by attorneys | 100,000 documents categorized as unlikely to be responsive and not reviewed by attorneys |
Once again, as given by our 95% CL and 5% MoE settings, we sample 383 documents of the 100,000 not reviewed. Coincidentally, we find the exact same proportion in this sample as in the other—5 responsive documents. As in the prior scenario, with 95% confidence we can infer that there are an additional 400 to 3000 responsive documents in the documents categorized as not responsive by our software.
As in the prior scenario, with 95% confidence we can infer that there are an additional 400 to 3000 responsive documents in the documents categorized as not responsive by our software.
However, low richness foils our efforts toward efficiency once again because this time we’re looking at the following lower and upper bounds:
With these numbers we’re back to validation metrics that may be less than defensible. It’s also worth noting that we should be transparent about calculating this range for recall as a function of the elusion rate rather than as a confidence interval around a sample proportion because the method of calculation implies certain assumptions, which I’ll save for a deeper dive on probability theory.
Now that we’ve demonstrated the problems with using a fixed sample size or even a fixed confidence interval for validation, we’ll use algebra to answer the question implicit in all this.
What sample size is appropriate for my elusion test?
In order to solve for our unknown (an appropriate sample size), we need to know the values of the following variables:
Total number of responsive documents identified
Total number of documents not slated for review or production
Target minimum recall
Expected elusion rate
The formula for the elusion rate is:
We’ll revisit the second scenario posed above and aim for 75% minimum recall as we determine our sample size. This sets the variables at:
4,000 = Total number of responsive documents identified
100,000 = Total number of documents not slated for review or production
75% = Target minimum recall
.65% = Expected elusion rate
The expected elusion rate can usually be estimated from other metrics, but if the elusion rate is unknown, 0 can be used for the smallest possible sample or use half of the value in step 2 below for a reasonable estimate. Also, note that of course you should continue fine-tuning your models and reviewing additional documents before sampling for elusion if your expected elusion rate is higher than the value in step 2.
Step 1) Solve for the maximum number of eluded documents permitted by your target recall:
Step 2) Calculate maximum elusion rate given by step 1:
Step 3) Solve for smallest possible sample size that allows us to estimate maximum elusion rate given by expected elusion rate and step 2 as upper bound. You can use the Wilson score interval formula below to solve for n—one day I’ll explain why that’s my preferred approach—or you can use an algorithm to solve for the sample size given by a Clopper-Pearson interval if you prefer.
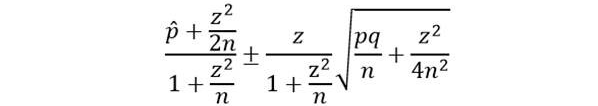
A sample of 1078 documents with no more than 7 responsive documents in it allows us to infer with 95% confidence that the actual elusion rate is below 1.33%.
Returning to our low richness scenario, our review team codes the elusion sample of 1078 documents with perfect accuracy and identifies 3 responsive documents in the sample. This indicates that with 95% confidence we can estimate the true elusion rate is .06% to .81%, thus it is reasonably likely there are 60 to 810 responsive documents in our discard pile.
Considering that,
Our elusion test allows us to estimate recall at 83% to 99%. While that range is quite a bit wider than one given by a 5% margin of error, it should be more than adequate for defensibility purposes.
Supposing that the true number of responsive documents in the total set for review was 4,500 out of 150,000 and our true recall was 89% (4,000 out of 4,500), we probably would have needed to sample around 5,000 documents for a control set to estimate recall with a 95% CL and a 5% MoE.
While very low richness still complicates validation, this approach to elusion testing gives us a more reasonable way to estimate recall.


